En ocasiones también conocida como secuencia de Fibonacci o incorrectamente como serie de Fibonacci, es en sí una sucesión matemática infinita. Consta de una serie de números naturales que se suman de a 2, a partir de 0 y 1. Básicamente, la sucesión de Fibonacci se realiza sumando siempre los últimos 2 números (Todos los números presentes en la sucesión se llaman números de Fibonacci) de la siguiente manera:
- 0,1,1,2,3,5,8,13,21,34...
Fácil, ¿no? (0+1=1 / 1+1=2 / 1+2=3 / 2+3=5 / 3+5=8 / 5+8=13 / 8+13=21 / 13+21=34...) Así sucesivamente, hasta el infinito. Por regla, la sucesión de Fibonacci se escribe así: xn = xn-1 + xn-2. Hasta aquí todo bien, pero de seguro estás preguntándote ¿quién fue Fibonacci?
¿Quién fue Fibonacci?
Bien, Fibonacci fue un matemático italiano del siglo XIII, el primero en describir esta sucesión matemática. También se lo conocía como Leonardo de Pisa, Leonardo Pisano o Leonardo Bigollo y ya hablaba de la sucesión en el año 1202, cuando publicó su Liber abaci. Fibonacci era hijo de un comerciante y se crió viajando, en un medio en donde las matemáticas eran de gran importancia, despertando su interés en el cálculo de inmediato.
Se dice que sus conocimientos en aritmética y matemáticas crecieron enormemente con los métodos hindúes y árabes que aprendió durante su estancia en el norte de África y luego de años de investigación, Fibonacci dió con interesantes avances. Algunos de sus aportes refieren a la geometría, la aritmética comercial y los números irracionales, además de haber sido vital para desarrollar el concepto del cero.
La sucesión de Fibonacci en la naturaleza
La secuencia de Fibonacci se encuentra en múltiples configuraciones biológicas, donde aparecen números consecutivos de la sucesión, como en la distribución de las ramas de los árboles, la distribución de las hojas en un tallo, los frutos de la piña tropical, las flores de la alcachofa, en las piñas de las coníferas, o en el "árbol genealógico" de las abejas melíferas. Sin embargo, también se han hecho muchas invocaciones infundadas a la aparición de los números de Fibonacci aprovechando su relación con el número áureo en la literatura popular.
Przemysław Prusinkiewicz avanzó la idea de considerar la sucesión de Fibonacci en la naturaleza como un grupo libre.
Un modelo del patrón de distribución de las semillas del girasol fue propuesto por H. Vogel en 1979. Presenta la forma
donde n es el índice de la flor y c es un factor de escala; entonces las semillas se alinean segúnespirales de Fermat. El ángulo de divergencia, de aproximadamente 137.51°, está relacionado con el número áureo. Debido a que el coeficiente es un número irracional, ninguna semilla tiene ninguna vecina al mismo ángulo respecto al centro, por lo que se compactan eficientemente. Debido a que las aproximaciones racionales al número aúreo son de la forma F(j):F(j + 1), los vecinos más próximos al número de semillas n están tods en n ± F(j) para cada índice j, que depende de r, la distancia al centro. Suele afirmarse que los girasoles y flores similares tienen 55 espirales en una dirección y 89 en la otra (o alguna otra pareja de números adyacentes de la sucesión de Fibonacci), pero esto sólo es cierto en ciertos rangos de radio, generalmente raros (y por ello más notables).
Otros links:
http://www.batanga.com/curiosidades/4461/que-es-la-sucesion-de-fibonacci
https://es.wikipedia.org/wiki/Sucesi%C3%B3n_de_Fibonacci
https://www.youtube.com/watch?v=WOSm4KxbHJk
https://www.youtube.com/watch?v=yDyMSliKsxI
https://www.youtube.com/watch?v=PZt7r9CbCaQ




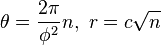




No hay comentarios:
Publicar un comentario