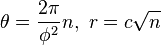INTEGRACIÓN DE LAS TIC Y LAS MATEMÁTICAS
Didáctica de las matemáticas
martes, 5 de julio de 2016
domingo, 29 de mayo de 2016
El cubo de rubik
Cubo de Rubik
El cubo de Rubik es un rompecabezas mecánico tridimensional inventado por el escultor y profesor de arquitectura húngaro Erno Rubik en 1974.Originalmente llamado "cubo mágico", el rompecabezas fue licenciado por Rubik para ser vendido por Ideal Toy Corp. en 1980. Ganó el premio alemán a mejor juego del año en la categoría "Mejor Rompecabezas" ese mismo año. Hasta enero de 2009 se han vendido 350 millones de cubos en todo el mundo, haciéndolo el juego de rompecabezas más vendido. Es considerado, en general, el juguete más vendido del mundo.
Un cubo de Rubik clásico, posee seis colores uniformes (tradicionalmente blanco, rojo, azul, naranja, verde y amarillo). Un mecanismo de ejes permite a cada cara girar independientemente, mezclando así los colores. Para resolver el rompecabezas, cada cara debe volver a consistir en un solo color.
Existen variaciones con diversos números de cuadrados por cara. Las principales versiones que hay son las siguientes: el 2×2×2 "Cubo de bolsillo", el 3×3×3 el cubo de Rubik estándar, el 4×4×4 (La venganza de Rubik), el 5×5×5 (El Cubo del Profesor) y desde septiembre de 2008 el 6×6×6 (V-Cube 6) y el 7×7×7 (V-Cube 7) de Verdes Panagiotis. La empresa Shengshou lanzó al mercado a principios de 2012 cubos de 8x8x8, 9x9x9 y 10x10x10. A partir de la fecha salen tanto nuevos productos como nuevas marcas. El gran salto de creación de cubos superiores a los 10x10x10 que había lanzado Shengshou en 2012, lo hizo la marca Moyu y Yuxin, lanzando las versiones, 11x11x11 (Yuxin) y 13x13x13 (Moyu) son las versiones producidas en masa más grandes hasta la fecha. También se pueden comprar versiones más grandes, por ejemplo el 17x17x17 producida por el diseñador Oskar Van Deventer. Incluso se ha llegado a crear un 22x22x22.
Mecanismo
Un cubo de Rubik estándar mide 5.7 cm en cada lado, aunque existen variaciones . El rompecabezas consiste en 26 piezas o cubos pequeños. Cada una incluye una extensión interna oculta que se entrelaza con los otros cubos, mientras les permite moverse a diferentes posiciones. Sin embargo, las piezas centrales de cada una de las seis caras son simplemente un cuadrado fijado al mecanismo principal. Esto provee la estructura para que las otras piezas quepan y giren alrededor. De este modo hay 21 piezas: una pieza central consistente de tres ejes que sostienen los seis centros cuadrados en su lugar pero dejando que giren y 20 piezas de plástico que caben en él para formar el rompecabezas montado.
NXN Clásicos
En esta familia son todos aquellos puzles cúbicos como el 3x3, es decir que n=x en la familia NXN entra en todos los cubos de mismo números de caras desde el 1x1, hasta el ya inventado 28x28.
Lo interesante es, que hay otros cubos NXN todavía no inventados tales como el 14x14, el 16x16, etc. Pero en esta familia especialmente se toman en cuenta los cubos 1x1 hasta el 13x13. Esto también se debe a que los otros cubos todavía no son fabricados en más pero por ser de mismo número de caras por vértices se toma cualquiera en cuenta.
Lista de NXN Clásicos existentes conocidos:
1x1, 2x2, 3x3, 4x4, 5x5, 6x6, 7x7, 8x8, 9x9, 10x10, 11x11, 12x12, 13x13, etc.
Matemática
Permutaciones
En el cubo de Rubik original (3×3×3) tiene ocho vértices y doce aristas. Hay 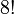 (40 320) formas de combinar los vértices del cubo. Siete de estas pueden orientarse independientemente, y la orientación de la octava dependerá de las siete anteriores, dando
(40 320) formas de combinar los vértices del cubo. Siete de estas pueden orientarse independientemente, y la orientación de la octava dependerá de las siete anteriores, dando 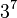 (2187) posibilidades. A su vez, hay
(2187) posibilidades. A su vez, hay 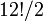 (239 500 800) formas de disponer las aristas, dado que una paridad de las esquinas implica asimismo una paridad de las aristas. Once aristas pueden ser volteadas independientemente, y la rotación de la duodécima dependerá de las anteriores, dando
(239 500 800) formas de disponer las aristas, dado que una paridad de las esquinas implica asimismo una paridad de las aristas. Once aristas pueden ser volteadas independientemente, y la rotación de la duodécima dependerá de las anteriores, dando  (2048) posibilidades. En total el número de permutaciones posibles en el Cubo de Rubik es de:
(2048) posibilidades. En total el número de permutaciones posibles en el Cubo de Rubik es de:
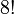 (40 320) formas de combinar los vértices del cubo. Siete de estas pueden orientarse independientemente, y la orientación de la octava dependerá de las siete anteriores, dando
(40 320) formas de combinar los vértices del cubo. Siete de estas pueden orientarse independientemente, y la orientación de la octava dependerá de las siete anteriores, dando 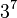 (2187) posibilidades. A su vez, hay
(2187) posibilidades. A su vez, hay 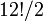 (239 500 800) formas de disponer las aristas, dado que una paridad de las esquinas implica asimismo una paridad de las aristas. Once aristas pueden ser volteadas independientemente, y la rotación de la duodécima dependerá de las anteriores, dando
(239 500 800) formas de disponer las aristas, dado que una paridad de las esquinas implica asimismo una paridad de las aristas. Once aristas pueden ser volteadas independientemente, y la rotación de la duodécima dependerá de las anteriores, dando  (2048) posibilidades. En total el número de permutaciones posibles en el Cubo de Rubik es de:
(2048) posibilidades. En total el número de permutaciones posibles en el Cubo de Rubik es de: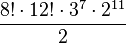 = 43 252 003 274 489 856 000
= 43 252 003 274 489 856 000
Es decir, cuarenta y tres trillones doscientos cincuenta y dos mil tres billones doscientos setenta y cuatro mil cuatrocientos ochenta y nueve millones ochocientos cincuenta y seis mil permutaciones.
El rompecabezas es a menudo promocionado teniendo solo "millardos" de posiciones, ya que números más grandes no son muy familiares para la mayoría de la gente.
Algoritmos
En la terminología de los aficionados al cubo de Rubik, una secuencia memorizada de movimientos que tiene un efecto deseado en el cubo es llamado algoritmo. Esta terminología deriva del uso matemático de algoritmo, un conjunto prescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permite realizar una actividad mediante pasos sucesivos. Cada método de resolver el cubo emplea su propio conjunto de algoritmos, junto a descripciones de cuál es el efecto del algoritmo, y cuándo puede ser usado para llevar al cubo a un estado más cercano a estar resuelto.
El
algoritmo para solucionar el cubo de rubik puede variar mucho dependiendo de
las diferentes posiciones o figuras que se vayan formando en cada una de las
caras del mismo, razón por la cual solo se mostraran unos links de la pagina de
videos de YouTube en los cuales se explican esto; además de un link para ver
algunos records armando el cubo y unas de sus variaciones.
https://www.youtube.com/watch?v=zR-0AipM87k
https://www.youtube.com/watch?v=CuIwaA7jtOcs
algoritmos.
https://www.youtube.com/watch?v=ZtmpzOi0wTs
.
Unidad dicatica
DIDÁCTICA IV: DE LAS
UNIDAD DIDÁCTICA: IDENTIDADES Y ECUACIONES
POR:
Alexis Vélez Orozco
LICENCIATURA EN MATEMÁTICAS Y FÍSICA
FACULTAD DE EDUCACIÓN
UNIVERSIDAD DE ANTIOQUIA
MEDELLÍN 2016
UNIDAD DIDÁCTICA DE MATEMÁTICAS
CURSO: Décimo Grado (10°)
TEMA: Identidades y ecuaciones trigonométricas
PRESENTACIÓN Y DESCRIPCIÓN GENERAL
En esta unidad didáctica se abordarán los temas de identidades y
ecuaciones trigonométricas, tratando de atender algunos contenidos que se
exigen en el currículo para el grado décimo, más aún se busca observar y
entender como las identidades y las ecuaciones trigonométricas facilitan mucho
la resolución de problemas, no solo en el aula de clase, si no en algunas
ocasiones problemas que se presentan en la vida cotidiana.
Los temas serán tratados comenzando con un poco de historia sobre ellos,
seguido de cómo se pueden deducir, luego se buscará aprender a resolver los
llamados ejercicios para familiarizarse con la parte procedimental y finalmente
se llevará a cabo la resolución de problemas cotidianos mediante la aplicación
de lo aprendido y trabajado.
El tiempo estimado será aproximadamente tres semanas, dependiendo que
tan rápido se pueda avanzar y de lo que ocurra durante el tiempo de clase.
ESTÁNDAR CURRICULAR
Describo y modelo fenómenos periódicos del mundo real usando relaciones
y funciones trigonométricas.
OBJETIVOS
Objetivos generales y específicos:
·
Se busca
que los estudiantes comprendan el concepto de
identidades trigonométricas mediante el análisis de las razones
trigonométricas.
·
Interpreten la noción de identidades trigonométricas y
que las resuelvan analíticamente.
·
reconozcan, analicen e interpretar las razones
trigonométricas y verifiquen su existencia.
·
Lograr
que los estudiantes se apropien de las identidades trigonométricas a partir de
su deducción desde las relaciones que hay entra las funciones trigonométricas
vistas desde la circunferencia unitaria y no unitaria.
·
Resuelvan
ecuaciones trigonométricas aplicando lo que son las identidades
trigonométricas.
·
Lograr
que los estudiantes resuelvan ecuaciones trigonométricas para valores
específicos.
·
Solucionen
problemas de la vida cotidiana aplicando las identidades trigonométricas, las
ecuaciones trigonométricas y además conceptos trabajados anteriormente.
RECURSOS
Para el desarrollo de las actividades se ha de utilizar:
1. El libro matemática experimental de 10, Julio
A. Uribe C.
2. Matemáticas Operativas, Luis H. Díez
3. Juegos matemáticos, hechos con cartón paja y
cartulina.
4. Fotocopias
5. Talleres
ANÁLISIS DE CONTENIDO
Desde lo epistemológico:
La trigonometría, al igual que cualquier otra rama de
la matemática, no fue el resultado de la labor de un solo hombre ni de una sola
nación.
Ya los antiguos
egipcios y babilonios conocían y habían utilizado propiedades o teoremas
relativos a las razones entre los lados de triángulos semejantes, sin
formularlos de una manera explícita, naturalmente. Dado que no nos encontramos
con ningún concepto de medida de ángulos en el mundo pre helénico, tales estudios
y consideraciones podrían quizás llamarse “trilaterometría” o medida de los
polígonos de tres lados, mejor que trigonometría o medida de las distintas
partes de un triángulo.
La mayoría de los
problemas de geometría que aparecen en los papiros hacen referencia a fórmulas
de medición necesarias para evaluar el área de figuras planas y de ciertos
volúmenes.
Los geómetras
egipcios parecen estar en condiciones de comprender la semejanza y la
proporcionalidad.
Hay división de opiniones acerca de si los babilonios estaban
familiarizados o no con el concepto de semejanza de figuras, aunque parece muy
probable que sí lo estuviesen. La semejanza entre todas las circunferencias
parece haber sido dada por descontado en Mesopotamia, como lo fue también en Egipto,
y los muchos problemas sobre triángulo que aparecen en las tablillas
cuneiformes parecen sugerir un cierto concepto de semejanza.
Desde lo fenomenológico:
Sin enfatizar en las identidades y ecuaciones
trigonométricas, se observa como la trigonometría a través de la historia a
permitido tratar gran cantidad de fenómenos, por ejemplo permite conocer la
altura de un árbol a partir de su sombra, en juegos que a simple vista parecen
simple como el billar, observándolo por lo físico, se puede tratar las
colisiones elásticas o in elásticas a partir de la trigonométrica, permitiendo
predecir inclusive las trayectorias resultantes en la colisión de partículas,
permite y facilita hallar distancias, cortas o largas, tan largas como lo
pueden ser las distancias entre los astros, permite diseñar planos, mapas, y
demás.
De este modo, unas correctas apropiaciones de los conceptos
trigonométricos, en muchas ocasiones pueden simplificar o facilitar algunos
aspectos o problemas de la vida.
ANÁLISIS DIDÁCTICO DE CONTENIDO
Para un buen desarrollo de las actividades a realizar durante
la enseñanza y el aprendizaje de lo relacionado a identidades y ecuaciones
trigonométricas se tiene pensado usar como apoyo didáctico diferentes
materiales, el objetivo es tratar de cambiar la idea o la posible imagen que
tienen los estudiantes acerca de que la matemática no puede ser divertida,
algunos de estos materiales son, un domino matemático, el cual permitirá
distraerse de lo operativo, pero a su vez permitirá memorizar de una manera
diferente algunas de las identidades trigonométricas principales, otro son un
grupo de cartas, las cuales vienen por parejas, y permitirán ayudar a la
familiarización con algunas identidades trigonométricas, inclusive se pueden
ampliar de un modo que permita trabajar las ecuaciones, otro materiales pueden
ser fotocopias, con talleres, libros en los cuales se explique y se trate la
parte teórica, entre otros.
ANÁLISIS COGNITIVO
Durante el desarrollo del contenido, se podrá observar las
fortalezas y las debilidades que tienen los estudiante no solo en las
identidades trigonométricas, sino también en conocimientos previos, como lo son
por ejemplo la resolución de problemas, la resolución de ecuaciones, la aplicación conocimientos previos en el desarrollo de
algunas actividades, la familiarización de los estudiantes con la parte teórica
de la matemática, se puede observar el desempeño de los alumnos en trabajos
grupales o individuales, que dificultades o fortalezas presentan a la hora de
trabajar conceptos, especialmente conceptos muy abstractos. Se podrá observar y
corregir los conceptos errados que se tengan; etc.
ANÁLISIS DE INSTRUCCIÓN
Para desarrollar cada una de las actividades, será necesario
alcanzar un nivel en el desarrollo y el manejo de conceptos previos, además una
óptima familiarización no solo con los algoritmos para el desarrollo de
problemas si no también con la parte teórica y conceptual. Es necesario además
que los estudiantes de una apropiada intervención acerca de cómo consideran que
se está llevando a cabo por parte del profesor la instrucción del contenido, es
decir, ayudar al maestro a impartir los conocimientos de manera que todos y
cada uno de los alumnos logre apropiarse adecuadamente de los contenidos.
SECUENCIA DE ACTIVIDADES
Actividades de introducción, motivación y diagnóstico:
En esta parte, se busca desarrollar una serie de actividades
que permitan a los estudiantes familiarizarse un poco con el contenido a ver y
además recordar los conocimientos previos necesarios para poder afrontar el
próximo contenido, en cuanto al profesor, le permitirán observar las dificultades
que presentan los estudiantes en cuanto a algunos conocimientos y de ser
posible afrontarlas y corregirlas.
Algunas actividades serán:
·
Juego de domino, diferentes
domino que permitan tratar temas previos, tales como un domino de funciones trigonométricas,
domino de funciones trigonométricas de cualquier ángulo, entre otros.
·
Juegos de memoria, como
cartas, que permitan emparejar funciones o ángulos con sus correspondientes, o
cartas que permitan identificar la relaciones entre grados y radianes, puede
ser también bingos con funciones trigonométricos, etc.
El tiempo estipulado para llevar a cabo estas actividades es
de entre una y dos horas.
Actividades de desarrollo:
En esta parte se busca que los estudiantes se apropien del
tema tratado y logren resolver ejercicios mediante la aplicación del conocimiento
adquirido unido a los conocimientos previos. Además, permitirán observar,
entender y corregir las falencias de los estudiantes en cuanto a los
procedimientos algorítmicos y en cuanto a la idea de conceptos previos o
actuales. Algunas de estas actividades son:
·
Talleres, con el objetivo de
familiarizarse con la parte algorítmica en la solución de ejercicios, y además
adueñarse de algunos conceptos que se trabajan mientras se desarrollan dichos
talleres.
·
Exposiciones, permitirían a
los estudiantes no solo el quedarse con los conocimientos trabajados en clase e
impartidos por el profesor, sino que además ayudara a que amplíen sus
horizontes y se adueñen de nuevos conceptos y aplicaciones de lo trabajado.
Entre otras actividades.
El tiempo estimado para el desarrollo de estas actividades es
de 5 horas, quizás más, quizás menos, dependiendo del desempeño de los
estudiantes.
Actividades de evaluación:
Para esta parte, principalmente se espera que los estudiantes
hayan tenido un buen desempeño en las actividades trabajadas previamente y
hayan tenido una óptima adquisición de los contenidos trabajados. Estas
actividades permitirían al profesor y a los alumnos que tan observar cuales son
los resultados de dicha adquisición de contenidos y cuáles son las fortalezas y
las debilidades no solo de los estudiantes si no de él mismo a la hora de
trabajar el contenido. Algunas de estas actividades son:
·
Quiz, los cuales durante
todo el trayecto en el cual se va trabajando permitirá observar y corregir las
principales falencias y además llenar vacíos de conocimientos previos.
·
Exámenes, permitirían
observar los resultados finales de todo el proceso de adquisición del
contenido, además de las mayores falencias y fortalezas con respecto a todo lo
trabajado.
El tiempo estimado en los quices es de unos 15 minutos por
quiz, y para los exámenes puede variar de 30 a 45 minutos.
domingo, 22 de mayo de 2016
En ocasiones también conocida como secuencia de Fibonacci o incorrectamente como serie de Fibonacci, es en sí una sucesión matemática infinita. Consta de una serie de números naturales que se suman de a 2, a partir de 0 y 1. Básicamente, la sucesión de Fibonacci se realiza sumando siempre los últimos 2 números (Todos los números presentes en la sucesión se llaman números de Fibonacci) de la siguiente manera:
- 0,1,1,2,3,5,8,13,21,34...
Fácil, ¿no? (0+1=1 / 1+1=2 / 1+2=3 / 2+3=5 / 3+5=8 / 5+8=13 / 8+13=21 / 13+21=34...) Así sucesivamente, hasta el infinito. Por regla, la sucesión de Fibonacci se escribe así: xn = xn-1 + xn-2. Hasta aquí todo bien, pero de seguro estás preguntándote ¿quién fue Fibonacci?
¿Quién fue Fibonacci?
Bien, Fibonacci fue un matemático italiano del siglo XIII, el primero en describir esta sucesión matemática. También se lo conocía como Leonardo de Pisa, Leonardo Pisano o Leonardo Bigollo y ya hablaba de la sucesión en el año 1202, cuando publicó su Liber abaci. Fibonacci era hijo de un comerciante y se crió viajando, en un medio en donde las matemáticas eran de gran importancia, despertando su interés en el cálculo de inmediato.
Se dice que sus conocimientos en aritmética y matemáticas crecieron enormemente con los métodos hindúes y árabes que aprendió durante su estancia en el norte de África y luego de años de investigación, Fibonacci dió con interesantes avances. Algunos de sus aportes refieren a la geometría, la aritmética comercial y los números irracionales, además de haber sido vital para desarrollar el concepto del cero.
La sucesión de Fibonacci en la naturaleza
La secuencia de Fibonacci se encuentra en múltiples configuraciones biológicas, donde aparecen números consecutivos de la sucesión, como en la distribución de las ramas de los árboles, la distribución de las hojas en un tallo, los frutos de la piña tropical, las flores de la alcachofa, en las piñas de las coníferas, o en el "árbol genealógico" de las abejas melíferas. Sin embargo, también se han hecho muchas invocaciones infundadas a la aparición de los números de Fibonacci aprovechando su relación con el número áureo en la literatura popular.
Przemysław Prusinkiewicz avanzó la idea de considerar la sucesión de Fibonacci en la naturaleza como un grupo libre.
Un modelo del patrón de distribución de las semillas del girasol fue propuesto por H. Vogel en 1979. Presenta la forma
donde n es el índice de la flor y c es un factor de escala; entonces las semillas se alinean segúnespirales de Fermat. El ángulo de divergencia, de aproximadamente 137.51°, está relacionado con el número áureo. Debido a que el coeficiente es un número irracional, ninguna semilla tiene ninguna vecina al mismo ángulo respecto al centro, por lo que se compactan eficientemente. Debido a que las aproximaciones racionales al número aúreo son de la forma F(j):F(j + 1), los vecinos más próximos al número de semillas n están tods en n ± F(j) para cada índice j, que depende de r, la distancia al centro. Suele afirmarse que los girasoles y flores similares tienen 55 espirales en una dirección y 89 en la otra (o alguna otra pareja de números adyacentes de la sucesión de Fibonacci), pero esto sólo es cierto en ciertos rangos de radio, generalmente raros (y por ello más notables).
Otros links:
http://www.batanga.com/curiosidades/4461/que-es-la-sucesion-de-fibonacci
https://es.wikipedia.org/wiki/Sucesi%C3%B3n_de_Fibonacci
https://www.youtube.com/watch?v=WOSm4KxbHJk
https://www.youtube.com/watch?v=yDyMSliKsxI
https://www.youtube.com/watch?v=PZt7r9CbCaQ
cubo de soma
Cubo Soma
 El Cubo Soma es un rompecabezas de disección sólido inventado por Piet Hein en 19331 durante una conferencia sobre la mecánica cuántica realizadas por Werner Heisenberg. Siete piezas hechas de cubos unitarios deben ser montadas en un cubo de 3x3x3. Las piezas también pueden ser utilizados para hacer una variedad de otras figuras 3D.
El Cubo Soma es un rompecabezas de disección sólido inventado por Piet Hein en 19331 durante una conferencia sobre la mecánica cuántica realizadas por Werner Heisenberg. Siete piezas hechas de cubos unitarios deben ser montadas en un cubo de 3x3x3. Las piezas también pueden ser utilizados para hacer una variedad de otras figuras 3D.
Las piezas del cubo Soma consisten en todas las posibles combinaciones de tres o cuatro unidades de cubos, unidas por sus caras, de tal manera que se forma al menos una esquina interior. Hay una combinación de tres cubos que satisface esta condición, y seis combinaciones de cuatro cubos que satisfacen esta condición, de los cuales dos son imágenes especulares entre sí (ver quiralidad). Por lo tanto, 3 + (6 x 4) es 27, que es exactamente el número de celdas de un cubo de 3 x 3 x 3.
El cubo Soma ha sido discutido detalladamente por Martin Gardner y John Horton Conway, y el libro Winning Ways for your Mathematical Plays (Vía a la victoria para su juego matemático), contiene un análisis detallado del problema del Cubo Soma. Hay 240 soluciones distintas del rompecabezas del cubo Soma, con exclusión de las rotaciones y reflexiones: éstas son fácilmente generadas por un sencillo programa de ordenador de búsqueda recursiva de vuelta atrás similar al utilizado para el rompecabezas de ocho reinas.
Las siete piezas del Cubo Soma, son todas policubos de orden tres o cuatro, en concreto, 6 de ellas están formadas por tetracubos y otra por el tricubo no lineal.
 El tricubo plano en forma de L
El tricubo plano en forma de L El Tetracubo plano en forma de T
El Tetracubo plano en forma de T El Tetracubo plano en forma de L
El Tetracubo plano en forma de L EL Tetracubo plano en forma de Z
EL Tetracubo plano en forma de Z El Tetracubo tridimensional en forma helicoidal dextrógira
El Tetracubo tridimensional en forma helicoidal dextrógira El Tetracubo tridimensional en forma helicoidal levógira
El Tetracubo tridimensional en forma helicoidal levógira El Tetracubo tridimensional en forma de tripode
El Tetracubo tridimensional en forma de tripode
Otros links:
https://www.youtube.com/watch?v=OFk4J4bSB54
http://ludoforum.com/el-cubo-soma-la-adiccion-de-piet-hein.html
https://www.youtube.com/watch?v=9ngzN2RQEtM
Suscribirse a:
Comentarios (Atom)
Entrada destacada
El cubo de rubik
Cubo de Rubik El cubo de Rubik es un rompecabezas mecánico tridimensional inventado por el escultor y profesor de arquitec...

-
David Paul Ausubel Nació en los Estados Unido s ( New York ), en el año de 1918, hijo de una familia judía emigrante de Euro...
-
Guy Brousseau Un importante investigador en un dominio determinante para la educación y la formación científicas Una vida el servicio...